Shamir’s Secret Sharing: A smarter way to protect your private keys

Private keys are like secret digital identity cards that prove who you are online. These complex strings of numbers and letters control access to digital assets like cryptocurrency and other data—and if you lose them or someone else gets hold of them, you’re in trouble.
Shamir’s Secret Sharing (SSS) is a smart way to protect sensitive information like private keys by breaking them into pieces. You only need a few of those pieces to put the secret back together. It’s built to keep your data safe, so no single person or location has full access to the secret.
In this guide, you’ll learn why security experts trust this method and how you can use it to strengthen your key management strategy. Whether you’re handling cryptocurrency wallets or protecting digital identities, understanding SSS can be an important step toward stronger privacy and control.
What is Shamir’s Secret Sharing?
SSS is a method for protecting sensitive information—like private keys—by breaking them into multiple pieces, or “shares.” You can safely give these shares to different people or store them in different places. The key part: you only need a certain number of shares (called a threshold) to recover the original secret.
The method was introduced in 1979 by Adi Shamir, a renowned cryptographer and co-inventor of RSA, one of the most widely used encryption systems. In his paper, “How to Share a Secret,” he proposed a clever solution to a common problem: how to keep a secret safe without relying on a single point of access or trust.
This secret sharing scheme exists in cybersecurity to reduce risk. If a full private key or password is stored in just one place, it can be lost, stolen, or misused. Doing cryptographic splitting, no single person or system has complete access, which helps guard against theft, human error, or technical failure.
The SSS algorithm is based on proven math, specifically polynomial equations, and the security and integrity of SSS are rooted in abstract algebra.
SSS doesn’t just split the data randomly; it guarantees that only a sufficient number of shares can recover the secret, and fewer than the threshold reveals nothing at all. It’s simple, effective, and doesn’t depend on hardware or trusted intermediaries.
How Shamir’s Secret Sharing works
As mentioned above, SSS takes something sensitive, like a password or a cryptographic key, and uses math to break it into several unique pieces. Each share looks like random data and reveals nothing on its own. But when you gather enough of them—say, 3 out of 5—you can initiate key reconstruction to see the original secret.
This kind of approach is especially relevant as more people adopt modern authentication tools like passkeys. By using secret sharing, you avoid a single point of failure—such as losing your device—because access can be securely distributed across multiple trusted parts.
One of the best parts of this approach is that the share threshold cryptography is flexible. You can set it based on how much trust or redundancy in key management you want. For example, if your threshold is 2 out of 5, that means any two shares are enough to recover the secret—but one alone is useless. This allows for both security and resilience. If a few shares are lost or one of the custodians can’t be reached, the secret is still recoverable as long as the threshold is met.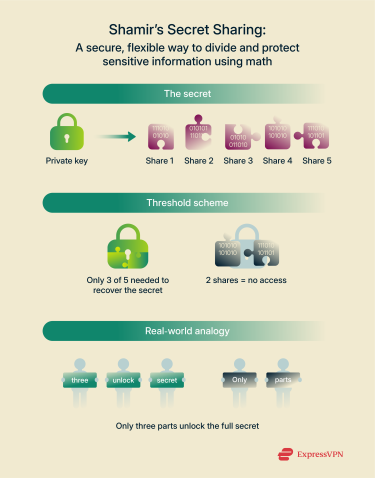 A major strength of Shamir’s method is that it doesn’t just split the secret; it protects each piece using a process called polynomial interpolation. That’s a fancy way of saying the secret is encoded using an equation, and only the right number of shares solves it. Each share is encrypted in such a way that even someone holding multiple shares—just under the threshold—can’t get any useful information.
A major strength of Shamir’s method is that it doesn’t just split the secret; it protects each piece using a process called polynomial interpolation. That’s a fancy way of saying the secret is encoded using an equation, and only the right number of shares solves it. Each share is encrypted in such a way that even someone holding multiple shares—just under the threshold—can’t get any useful information.
You can even set a hierarchy so that more trusted members can have more shares and vice versa. And since no single share contains usable data, there’s little risk if a piece falls into the wrong hands—especially when dealing with untrusted or unknown custodians.
Why use Shamir’s Secret Sharing?
SSS solves two big problems: how to keep a private key safe and how to avoid total loss if one part of the key goes missing. Traditional methods like storing a key in one place or writing it down leave you vulnerable to theft, hardware failure, or human error. Shamir’s method spreads the risk, making it much harder for anyone, or anything, to compromise your key.
Stronger protection for private keys
Instead of depending on a single file, password, or hardware device, Shamir’s Secret Sharing creates a multi-part system to which no one has full access. Even if someone steals one piece, they can’t do anything with it unless they get enough of the others, too. This reduces the chances of accidental exposure or targeted attacks.
Built-in resilience if something goes wrong
Since you don’t need every piece to recover your secret, you’re protected if one share gets lost or damaged. For example, if you create five shares and only need three to restore your key, two can go missing, and you’re still safe. That built-in flexibility makes the system reliable, even when things get messy.
More control over who gets access
You can choose who gets a share and how many are needed to unlock the secret. This means you’re not putting all your trust in one person, service, or device. You can involve trusted family members, secure locations, or offline backups—tailoring the setup to your comfort level and trust network.
Where Shamir’s Secret Sharing is used today
Shamir’s Secret Sharing isn’t just a theory—it’s used in real-world tools and systems to keep sensitive data safer. From crypto wallets to cloud services, this method helps people and organizations manage secrets without putting everything in one place.
Securing cryptocurrency wallets
The crypto wallet scamming scene is huge, and SSS is one of the most popular methods of protecting crypto wallets against these threats. If someone loses their wallet’s private key, the funds are gone forever. Shamir’s method lets users split the secret into multiple parts—some can be stored offline, others given to trusted people. You only need a few to recover the wallet, so you’re covered even if one gets lost.
Sharing access in the cloud
Cloud-based services sometimes use secret sharing to give multiple stakeholders access to sensitive data without giving full control to any single person. For example, a company storing encrypted files might give pieces of the decryption key to several executives. Only when enough of them agree can the files be unlocked.
Managing keys across teams or devices
In larger organizations or security-focused setups, SSS can spread access across different team members or hardware devices. This prevents any one employee, device, or breach from compromising the whole system. It’s especially useful in IT environments where shared control and redundancy are critical.
Emergency recovery and backup systems
Some services use Shamir’s method as part of their backup or account recovery process. If you lose access to a device or app, you can use pieces stored elsewhere—like on a USB drive, with a trusted contact, or even printed and locked in a safe—to get back in. This avoids the need for risky single-password resets.
How Shamir’s Secret Sharing compares to other protection methods
Shamir’s Secret Sharing differs from other methods by offering better flexibility, stronger security, and a lack of dependency on a single point of failure.
Traditional backup options
Typical backups often involve saving a private key in one or two places—on paper, in a password manager, in cloud storage, or via another threshold-based backup option. While simple and convenient, these options have drawbacks and limitations.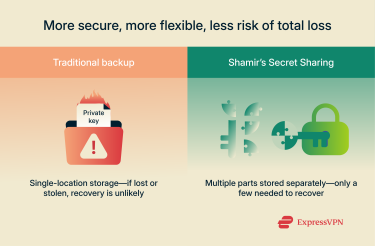 One such drawback is lost data. For example, if you lose your private key or someone steals it, recovery becomes impossible, mostly because these methods tend to rely on a single backup location or service. Shamir’s method avoids that by splitting the secret into multiple chunks that you can use to reinstate the data even if you don’t have access to all the pieces.
One such drawback is lost data. For example, if you lose your private key or someone steals it, recovery becomes impossible, mostly because these methods tend to rely on a single backup location or service. Shamir’s method avoids that by splitting the secret into multiple chunks that you can use to reinstate the data even if you don’t have access to all the pieces.
Hardware security modules (HSMs)
Hardware security modules (HSMs) store private keys inside secure physical devices built to resist tampering. They're often used by healthcare, financial, and defense institutions that need to meet strict security standards.
That said, they come with their own set of drawbacks. For starters, they’re expensive and hard to scale across multiple environments. Secondly, if the device fails or is mismanaged, the keys can be lost or exposed.
In contrast to SSS, HSMs are for when you don’t want to share a secret with others, and they help to keep the secret in a place where it’s not accessible. SSS, on the other hand, involves sharing parts of a secret with others by default.
Shamir’s method vs. other threshold systems
Other threshold-based systems—like Threshold Signature Schemes (TSS)—take secret sharing a step further. Instead of putting the secret back together, TSS lets people use their pieces to perform actions like signing a message without ever fully revealing the secret key.
This approach adds some complexity and can be slower, but it’s especially useful in situations like managing a blockchain wallet, where you want multiple people to approve a transaction without anyone seeing the full private key. 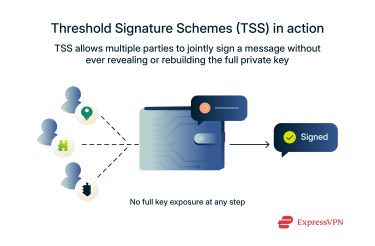 Another option is multi-sig, short for multi-signature. It’s a way to split control over a wallet or transaction so that multiple people have to agree before anything goes through. For example, imagine a business account where three out of five team members must approve a transfer. This setup adds a strong layer of security and keeps everyone accountable, since no one can act alone.
Another option is multi-sig, short for multi-signature. It’s a way to split control over a wallet or transaction so that multiple people have to agree before anything goes through. For example, imagine a business account where three out of five team members must approve a transfer. This setup adds a strong layer of security and keeps everyone accountable, since no one can act alone.
The trade-off is that it can be slower and less flexible, since all the required parties need to take action. That’s great for team decisions but less ideal if someone is unavailable or uncooperative.
In contrast, Shamir’s method is lightweight and proven—it doesn’t need constant connectivity, special hardware, or trusted third parties. It’s also easier to understand and implement, which makes it more accessible for individuals and small teams looking for strong protection without the overhead. Like many modern techniques, it’s built on foundational cryptographic ideas that trace back through history, as seen in the evolution of encryption.
What to know before you use Shamir’s Secret Sharing
While Shamir’s Secret Sharing is a powerful tool, it isn’t foolproof. Like any security method, it requires careful planning and smart handling. Knowing how to set it up correctly—and understanding the trade-offs—can make the difference between strong protection and unintended loss.
Risks and limitations to consider
The biggest risk with SSS is mismanaging the shares. If you lose too many and drop below the required threshold, the secret becomes unrecoverable, and it’s gone for good. On the flip side, if an attacker gets hold of enough shares to meet the threshold, they can piece together your secret and potentially access sensitive data. Another limitation is that Shamir’s method doesn’t have a built-in way to revoke or update shares. Once the shares are out there, you can’t just “deactivate” one if something changes—like if a trusted contact becomes unavailable or untrustworthy. You’d need to reconstruct the secret and generate new shares from scratch.
Another limitation is that Shamir’s method doesn’t have a built-in way to revoke or update shares. Once the shares are out there, you can’t just “deactivate” one if something changes—like if a trusted contact becomes unavailable or untrustworthy. You’d need to reconstruct the secret and generate new shares from scratch.
That’s why it’s so important to treat shares carefully, not just where you store them, but how you manage changes over time. A solid setup today might need updating tomorrow, and the method requires planning to handle that securely.
Setting the right threshold for recovery
Deciding how many shares you need to recover your secret is a key part of setting up Shamir’s Secret Sharing. Here’s how to think about it:
- Set the threshold too low: It becomes easier for someone to misuse the secret if they get access to just a few shares.
- Set the threshold too high: You risk locking yourself out if you lose too many shares and can’t meet the minimum required to recover the secret.
- Aim for a balanced setup: For example, generate 6 total shares and require 4 to recover the secret. This gives you redundancy in case 1 or 2 shares are lost and protection against any one person accessing the secret alone.
How to store shares safely
Each share should be treated like a critical piece of your digital identity. Don’t keep them all in one place, and don’t rely solely on digital storage, which can be hacked, corrupted, or lost. Instead, diversify how and where you store them: maybe one goes on an encrypted USB drive, another with a trusted family member, a third in a printed copy stored in a safe, and a fourth in an offline vault.
While each share is individually encrypted and meaningless on its own, it still needs protection. Someone getting access to one share shouldn’t pose a risk, but it’s still best to avoid that scenario altogether. Spread out your shares across different locations—your home, a bank, or with trusted contacts—so if something happens to one, you won’t lose access to your secret.
The whole point of Shamir’s Secret Sharing is to eliminate single points of failure. Storing shares thoughtfully helps you stay in control while keeping your most sensitive data secure and recoverable.
FAQ: Common questions about Shamir’s Secret Sharing
What’s the minimum number of shares needed?
At least two shares are needed. Shamir’s Secret Sharing requires a minimum of two shares to reconstruct a secret because the system relies on mathematical formulas that need at least that many data points to work. You can choose a higher threshold depending on how secure or flexible you want the system to be.
Can I use SSS to protect biometric or personal data?
The method works with any type of digital secret, including encrypted biometric files or sensitive personal information. However, the data should first be converted into a format that can be split, typically an encryption key or password protecting the actual data. This adds an extra layer of protection without storing the biometric data itself in fragmented form.
Is SSS more secure than regular encryption?
Shamir’s Secret Sharing doesn’t encrypt data—it protects the encryption key itself by splitting it into parts. When used together with strong encryption like Pretty Good Privacy (PGP), unauthorized access is made much harder by removing single points of failure. It's most effective as part of a layered security strategy, not a standalone solution.
What happens if a share is lost?
If a share is lost, the secret can still be recovered, as long as you have enough remaining shares. The threshold system allows you to set how many shares are needed to reconstruct the secret. For example, if you create 5 shares and only need 3 to recover the key, losing one or two won’t cause any problems. But if the number of available shares drops below the threshold, the secret is unrecoverable.
Are there any known weaknesses in the SSS method?
The method itself is considered mathematically strong, but its weaknesses lie in how it’s implemented or managed. Shamir’s Secret Sharing is built on solid cryptographic principles, but risks can arise if shares are stored insecurely or if the threshold is poorly chosen.
In addition, if the secret distribution of shares isn’t well planned, risks can arise as well. Human error, physical theft, or failure to update shares during key changes are common vulnerabilities—not flaws in the method, but in how it's used.
How is SSS used in real-world situations?
Shamir’s Secret Sharing is used in all kinds of real-world situations where data security matters. For example, cryptocurrency wallets use it to split a private key into parts stored in different places—so even if one location is compromised, the key stays safe.
Cloud services might use it to let several team members access encrypted data without giving full control to any single person. And in larger organizations, it’s often used to manage backup or recovery keys by spreading access across multiple trusted parties or devices.
Take the first step to protect yourself online. Try ExpressVPN risk-free.
Get ExpressVPN